When you look at your surrounding environment, it might seem like youre living on a flat plane.
This is likely why some people in the past believed the earth to be flat.
But most people now know that is far from the truth.

© vkulieva/iStock via Getty Images Plus
What other possible spaces might you be living on?
That is, what other spaces around you are 2D?
For example, the surface of a giant doughnut is another 2D space.
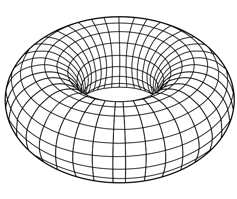
A doughnut, also called a torus, is a shape that you can move across in two directions, just like the surface of the Earth.
Through a field called geometric topology,mathematicians like mestudy all possible spaces in all dimensions.
Over a century ago, mathematicians figured outall the possible 2D spacesand many of their properties.
In the past several decades, mathematicians have learned a lot about all of the possible 3D spaces.
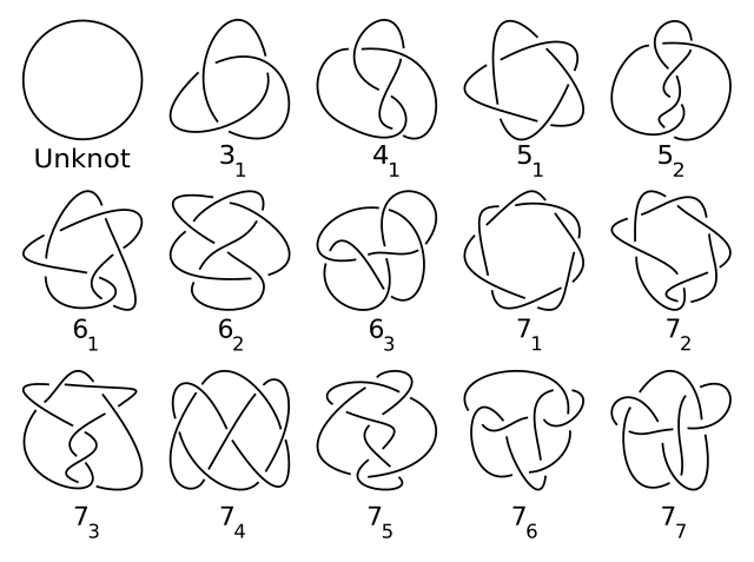
Knots are examples of spaces that sit inside other spaces.
While we do not have a complete understanding like we do for 2D spaces, we doknow a lot.
With this knowledge, physicists and astronomers can make a run at determine what3D space people actually live in.
While the answer is not completely known, there are manyintriguing and surprising possibilities.

The options become even more complicated if you consider time as a dimension.
These four numbers are what make up a 4D space.
But a branch of physics calledstring theorysuggests that the universe has many more dimensions than four.

There are also practical applications of thinking about higher dimensional spaces, such asrobot motion planning.
Suppose you are trying to understand the motion of three robots moving around a factory floor in a warehouse.
it’s possible for you to interpret the possible positions of the robots as a 6D space.

As the number of robots increases, the dimension of the space increases.
Factoring in other useful information, such as the locations of obstacles, makes the space even more complicated.
to make it study this problem, you’re gonna wanna study high-dimensional spaces.

Such loops are called mathematical knots.
Thestudy of knotsfirst grew out of physics but has become a central area of topology.
In addition, knots have many applications, ranging fromstring theoryin physics toDNA recombinationin biology tochiralityin chemistry.

What shape do you live on?
Topology is currently useful in science and engineering.
News from the future, delivered to your present.

Are We Inside a Black Hole?
















